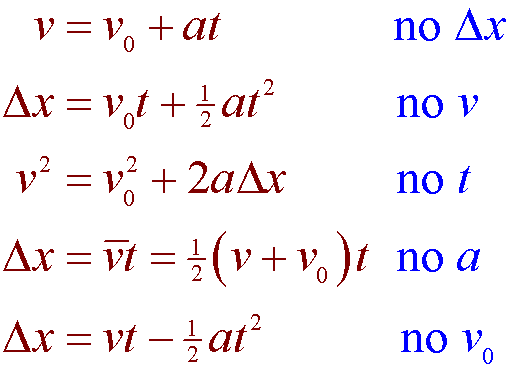Nice Distance Kinematic Equation

Calculus is an advanced math topic but it makes deriving two of the three equations of motion much simpler.

Distance kinematic equation. Q1 equation of motion is given x 2t² find the speed at 2s and find average speed at 2s. To determine this equation we recall a familiar kinematic equation for translational or straight-line motion. In introductory mechanics there are three equations that are used to solve kinematics problems.

KE 1 2 mv2 KE kinetic energy. We have already studied kinematic equations governing linear motion under constant acceleration. By definition acceleration is the first derivative of velocity with respect to time.

Thus we have five motion parameters. The distance traveled can be found by a calculation of the area between the line on the graph and the time axis. The kinematic equations are a set of four equations that can be utilized to predict unknown information about an objects motion if other information is known.

Yes youre first equation d V i t 1 2 a t 2 is saying that the total distance is the initial velocity times time plus one half times the acceleration times time squared Now the only difference between this and the second equation is obviously the d i. Because velocity is the antiderivative of acceleration that means that v t a t and v t int a t. It is derived using the kinematics equations.

Kinematics is the description of motion. Ans this equation relation is between distance and time now from basic kinematics concept and parameter we know that dxdt v if you have not study differentiation refer differentiation post. Area 05bh 05 250 s 250 ms Area 313 m.

D v t 12 a t 2. First we need to establish that acceleration is represented by the equation a t -98. Initial velocity Vo final velocity V acceleration a time t and displacement S and two equations.